Ein neuer Ansatz bringt frischen Schwung in „Dijkstras Algorithmus“, ein jahrzehntealtes Grundproblem der Informatik.

Xinkai Shu erhält gemeinsam mit Kolleginnen und Kollegen einen Best Paper Award der STOC 2025. Foto: Philipp Zapf-Schramm/MPI INF
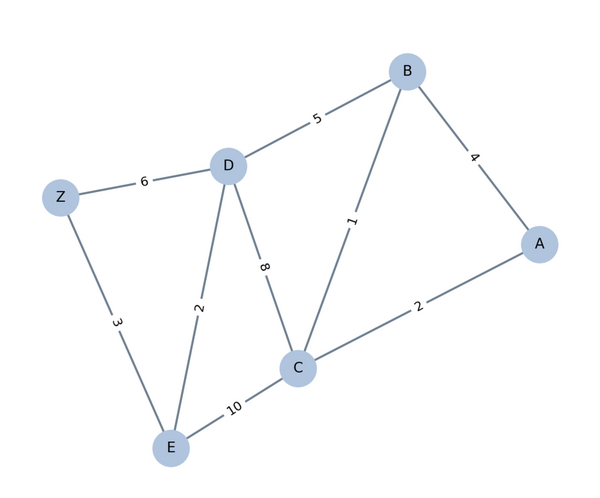
Graphen sind ein Konzept aus der Informatik, mit dem sich Beziehungen zwischen verschiedenen Entitäten modellieren lassen. Sie eignen sich, um reale Systeme wie Verkehrsnetze, soziale Netzwerke oder neuronale Verbindungen im Gehirn abzubilden. Ein internationales Forschungsteam unter Beteiligung des Saarbrücker Max-Planck-Instituts für Informatik hat nun einen Algorithmus entwickelt, der solche Netzwerke schneller verarbeiten kann als namhafte bisherige Verfahren, insbesondere „Dijkstras Algorithmus“. Für diese Leistung wurde das Team auf einer der weltweit führenden Konferenzen der theoretischen Informatik mit einem „Best Paper Award“ ausgezeichnet.
Graphen lassen sich gut mit Straßenkarten vergleichen. In einem Graphen stehen Punkte, sogenannte Knoten, für Orte, etwa Städte oder Kreuzungen. Linien, die sogenannten Kanten, verbinden diese Punkte und können mit Zahlen versehen sein, die zum Beispiel Entfernungen, Fahrzeiten oder Mautkosten angeben. So entsteht ein abstraktes Modell, das, wie in diesem Fall, ein reales Verkehrsnetz beschreibt. Ein zentrales Problem der theoretischen Informatik besteht darin, in einem solchen Netzwerk den kürzesten oder günstigsten Weg von einem Startpunkt zu allen anderen Punkten zu finden. In der Fachwelt spricht man dabei vom „Single-Source Shortest-Paths Problem (SSSP)“. Genau diese Aufgabe lösen auch Navigationssysteme, wenn sie eine Route berechnen – etwa vom aktuellen Standort zu allen erreichbaren Zielen.
Ein grundlegender Algorithmus zur Lösung dieses Problems ist „Dijkstras Algorithmus“, benannt nach dem niederländischen Informatiker Edsger Dijkstra. Seit seiner Entwicklung im Jahr 1956 gilt der Algorithmus als wegweisend. Mit ihm lässt sich effizient ermitteln, welche Wege durch das Netzwerk am wenigsten kosten – sei es beispielsweise in Kilometern, Minuten oder anderen Maßzahlen. Er beginnt bei einem Startknoten und untersucht schrittweise alle erreichbaren Verbindungen, wobei stets die aktuell nächste Verbindung gewählt wird. Sobald der kürzeste Weg zu einem Punkt gefunden ist, wird dieser nicht mehr verändert. So breitet sich die Suche iterativ aus, bis alle erreichbaren Punkte erfasst sind.
Um Dijkstras Algorithmus zu verbessern, betrachtet das neue Paper den Teil, der für einen Großteil des Rechenaufwands verantwortlich ist: die Interaktion mit der sogenannten „Priority Queue“. Während seiner Ausführung muss Dijkstras Algorithmus eine sogenannte „Frontier“ verwalten – also die Menge an Knoten, die bereits entdeckt, aber noch nicht vollständig verarbeitet wurden. Für diese Knoten ist die aktuell kürzeste bekannte Distanz zur Startposition bekannt, doch ihre Nachbarn wurden noch nicht vollständig überprüft. Diese Knoten werden in einer „Priority Queue“ gespeichert, aus der jeweils der aktuell am nächsten gelegene Knoten entnommen wird. Die „Frontier“ kann dabei bis zu "n" Knoten umfassen, wobei n die Anzahl der Knoten im gesamten Netzwerk ist. Das Entnehmen eines Knotens verursacht einen Aufwand von log(n) pro Operation, was insgesamt zu einer Laufzeit von n log(n) führt.
„Unser neuer Algorithmus reduziert die Größe der betrachteten „Frontier“ schrittweise mithilfe einer rekursiven Methode, die Elemente aus Dijkstras Algorithmus mit einem weiteren bekannten Verfahren – dem sogenannten Bellman-Ford-Algorithmus – kombiniert. Außerdem verwenden wir eine speziell entworfene Datenstruktur, mit der sich Gruppen von Knoten einfügen und entnehmen lassen“, erklärt Xinkai Shu, Postdoktorand in der Abteilung „Algorithms and Complexity“ am Max-Planck-Institut für Informatik in Saarbrücken unter der Leitung von Professor Danupon Nanongkai. Dadurch lässt sich die Anzahl Operationen deutlich verringern, was die Laufzeit des Algorithmus verbessert.
Für ihre Arbeit mit dem Titel „Breaking the Sorting Barrier for Directed Single-Source Shortest Paths“ wurden Xinkai Shu und seine Co-Autoren Ran Duan, Jiayi Mao und Longshui Yin (alle Tsinghua-Universität Beijing) sowie Xiao Mao (Stanford University) auf dem „ACM Symposium on Theory of Computing“ (STOC) 2025, einer der führenden Konferenzen der theoretischen Informatik, mit einem „Best-Paper-Award“ ausgezeichnet. Gewürdigt werden damit insbesondere Beiträge, die eine neue, starke Methode einführen, ein lange ungelöstes Problem lösen, oder ein neues, bedeutendes Problem formulieren und lösen. Der Preis wird am 23. Juni auf der Konferenz in Prag vergeben.
Originalpublikation:
Ran Duan, Jiayi Mao, Xiao Mao, Xinkai Shu, Longhui Yin (2025): „Breaking the Sorting Barrier for Directed Single-Source Shortest Paths“. 57th Annual ACM Symposium on Theory of Computing (STOC).
Redaktion und Kontakt:
Philipp Zapf-Schramm
Max-Planck-Institut für Informatik
Tel: +49 681 9325 5409
E-Mail: pzs@mpi-inf.mpg.de